CAMBRIDGE A&AS LEVEL
A&AS LEVEL KONULARI
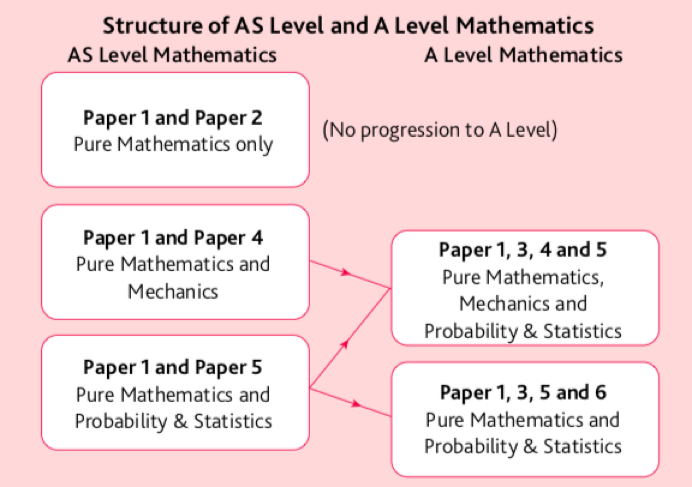
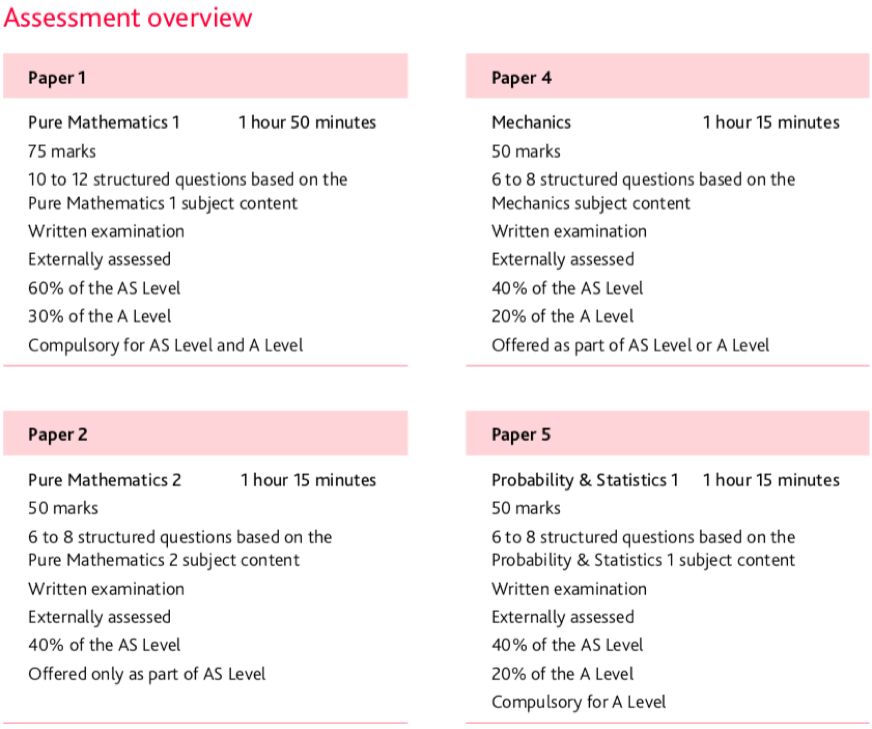
PURE MATHEMATICS 1 :
- QUADRATICS
- FUNCTIONS
- COORDINATE GEOMETRY
- CIRCULAR MEASURE
- TRIGONOMETRY
- SERIES
- DIFFERENTIATION
- INTEGRATION
PURE MATHEMATICS 2 :
- ALGEBRA
- LOGARITHMIC AND EXPONENTIAL FUNCTIONS
- TRIGONOMETRY
- DIFFERENTIATION
- INTEGRATION
- NUMERICAL SOLUTION OF EQUATIONS
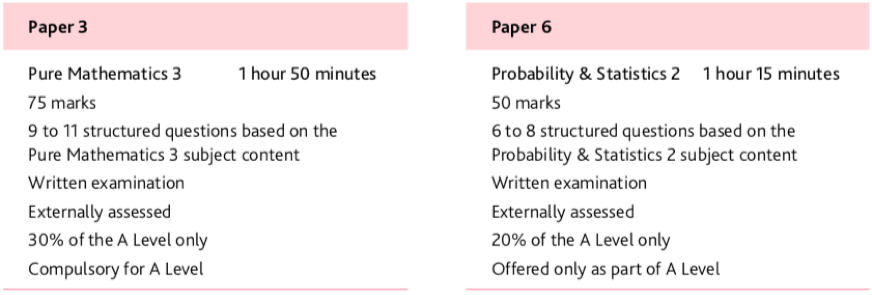
PURE MATHEMATICS 3 :
- ALGEBRA
- LOGARITHMIC AND EXPONENTIAL FUNCTIONS
- TRIGONOMETRY
- DIFFERENTIATION
- INTEGRATION
- NUMERICAL SOLUTION OF EQUATIONS
- VECTORS
- DIFFERENTIAL EQUATIONS
- COMPLEX NUMBERS
MECHANICS :
- FORCES AND EQUILIBRIUM
- KINEMATICS OF MOTION IN A STRAIGHT LINE
- MOMENTUM
- NEWTON’S LAWS OF MOTION
- ENERGY, WORK AND POWER
PROBABILITY&STATISTICS 1 :
- REPRESENTATION OF DATA
- PERMUTATIONS AND COMBINATIONS
- PROBABILITY
- DISCRETE RANDOM VARIABLES
- THE NORMAL DISTRIBUTION
PROBABILITY&STATISTICS 2 :
- THE POISSON DISTRIBUTION
- LINEAR COMBINATIONS OF RANDOM VARIABLES
- CONTINUOUS RANDOM VARIABLES
- SAMPLING AND ESTIMATION
- HYPOTHESIS TESTS
A&AS LEVEL HAKKINDA
Öğrencilere çeşitli Cambridge Uluslararası AS & A Düzeyleri sunarak, onlara en çok takip etmek istedikleri eğitim yolunu bulma şansı verebilirsiniz. Aralarından seçim yapabileceğiniz 50’den fazla konu ile öğrenciler sevdikleri ve en iyi oldukları derslerle eğitimlerine devam edebilirler.
Bir Cambridge Uluslararası AS & A Seviye programının takip edilmesi, öğrencilerin aşağıdakiler de dahil olmak üzere üniversitelerin çok değer verdiği yeteneklerini geliştirmelerine yardımcı olur:
• Konularının derinlemesine anlaşılması
• Üst düzey düşünme becerileri – analiz, eleştirel düşünme, problem çözme
• Düzenli ve tutarlı argümanlar sunmak
• Bağımsız öğrenme ve araştırma.
Cambridge International AS & A Level Mathematics için temel kavramlar:
Problem çözme:
Matematik temel olarak problem çözme ve sistemleri ve modelleri farklı şekillerde çözümlemedir. Bunlar:
- Cebir: Bu, matematiksel akıl yürütmeyi destekleyen ve ifade eden ve bir dizi bağlamda genelleme için bir araç sağlayan önemli bir araçtır.
- Geometrik Teknikler: Cebirsel temsiller, bize bir durumu anlamamız için yeni bir yol sağlayan mekansal bir ilişkiyi de tanımlar.
- Analiz: Bu, dinamik durumlarda değişimi tanımlayan ve fonksiyonlar ile grafikler arasındaki bağlantıların altını çizen temel bir unsurdur.
- Mekanik Modeller: Bunlar, parçacıkların ve nesnelerin kuvvetlerin etkisi altında nasıl hareket ettiğini veya sabit kaldığını açıklar ve tahmin eder.
- İstatistiksel Yöntemler: Bunlar etrafımızdaki dünyanın yönlerini ölçmek ve modellemek için kullanılır. Olasılık teorisi, şans olaylarının nasıl ilerleyebileceğini ve şans hakkındaki varsayımların kanıtlarla gerekçelendirilip gerekçelendirilmediğini tahmin eder.
İletişim:
Matematiksel kanıt ve muhakeme cebir ve notasyon kullanılarak ifade edilir, böylece diğerleri her bir muhakeme çizgisini takip edebilir ve bütünlüğünü ve doğruluğunu doğrulayabilir. Matematiksel gösterim evrenseldir. Her çözüm yapılandırılmıştır, ancak kanıt ve problem çözme de yaratıcı ve özgün düşünceyi davet etmektedir.
Matematiksel modelleme:
Matematiksel modelleme, birçok farklı durum ve probleme uygulanabilir ve tahminlere ve çözümlere yol açar. Modeli oluşturmak için çeşitli matematiksel içerik alanları ve teknikleri gerekebilir. Model oluşturulduktan ve uygulandıktan sonra, sonuçlar gerçek dünya hakkında tahminler ve bilgiler vermek üzere yorumlanabilir.
SINAVLAR HAKKINDA
Daha önceki yıllarda yapılmış sınavlara (Past Papers) aşağıdaki linkten ulaşabilirsiniz.